TL;DR: In RLHF, there is a tension between the reward learning phase, which uses human preferences as a form of comparison, and the RL fine-tuning phase, which optimizes a single non-comparison reward. What if we do RL as a comparison method?
Figure 1:
This diagram shows the difference between reinforcement learning and reinforcement learning. pure feedback and relative feedback. By incorporating a new component, pairwise policy gradients, we can integrate the reward modeling phase and the RL phase, enabling direct updates based on pairwise responses.
Large language models (LLMs) have supported increasingly capable virtual assistants, such as GPT-4, Claude-2, Bard, and Bing Chat. These systems can respond to complex user queries, write code, and even produce poetry. The technology behind these amazing virtual assistants is Reinforcement Learning with Human Feedback (RLHF). RLHF aims to align models to human values and eliminate unintended behavior that can often result from models being exposed to large amounts of low-quality data during the pre-training phase.
Proximal Policy Optimization (PPO), the dominant RL optimizer in this process, has been reported to exhibit instability and implementation complexity. More importantly, there are persistent inconsistencies in the RLHF process. Even though the reward model is trained using comparisons between different responses, the RL fine-tuning step operates on individual responses without making comparisons. These inconsistencies can make matters worse, especially in the difficult area of language production.
Considering this background, interesting questions arise. Is it possible to design an RL algorithm that learns in a comparative manner? To explore this, we introduce Pairwise Proximal Policy Optimization (P3O), a method that harmonizes the training process in both the reward learning phase of RLHF and the RL fine-tuning phase, which provides a satisfactory solution to this problem.
background
Figure 2:
The three stages of RLHF are explained in the OpenAI blog post. As shown on the left side of Figure 1, the third step belongs to reinforcement learning with absolute feedback.
In a traditional RL setting, rewards are either specified manually by the designer or provided by a well-defined reward function, as in Atari games. However, defining a good reward to steer a model toward useful and harmless responses is not straightforward. RLHF solves this problem by learning a reward function from human feedback, especially in the form of comparisons, and then applying RL to optimize the learned reward function.
The RLHF pipeline is divided into several stages in detail:
Supervised fine-tuning phase: Pre-trained models undergo maximum likelihood loss on high-quality datasets and learn to answer human queries through imitation.
Reward Modeling Step: The SFT model prompts \(x\) to generate pairs of answers \(y_1,y_2\sim \pi^{\text{SFT}}(y\vert x)\). The generated responses form a data set. Response pairs are presented to a human labeler who expresses a preference for one answer over the other, denoted by \(y_w \succ y_l\). We then use the comparison loss to train the reward model \(r_\phi\).
\(\mathcal{L}_R = \mathbb{E}_{(x,y_l,y_w)\sim\mathcal{D}}\log \sigma\left(r_\phi(y_w|x)-r_\phi (y_l|x)\right)\)
RL fine tuning steps: The SFT model serves as the initialization for this step, and the RL algorithm optimizes the policy to maximize reward while limiting deviation from the initial policy. Formally, this is done via:
\(\max_{\pi_\theta}\mathbb{E}_{x\sim \mathcal{D}, y\sim \pi_\theta(\cdot\vert x)}\left(r_\phi(y\ vertical x)-\beta D_{\text{KL}}(\pi_\theta(\cdot\vert x)\Vert \pi^{\text{SFT}}(\cdot\vert x))\right)\ )
The inherent problem with this approach is that the rewards are not unique. For example, given a reward function \(r(y\vert x)\), simply shifting the prompt reward to \(r(y\vert x)+\delta(x)\) produces another valid reward It’s possible. function. These two reward functions result in the same loss for all response pairs, but are significantly different when optimized using RL. In extreme cases, if the added noise increases the range of the reward function, the RL algorithm may be misled into increasing the likelihood of responding with a higher reward, even if that reward is meaningless. That is, the reward size information in the prompt \(x\) may cause the policy to break, but it may not learn anything useful (relative preferences represented by reward differences). To solve this problem, our goal is to develop the following RL algorithm: Invariant to compensated translations.
Induction of P3O
Our idea came from Vanilla Policy Gradient (VPG). VPG is a widely adopted first-order RL optimizer due to its simplicity and ease of implementation. In the Contextual Bandit (CB) setting, the VPG is formulated as follows:
\(\nabla \mathcal{L}^{\text{VPG}} = \mathbb{E}_{y\sim\pi_{\theta}} r(y|x)\nabla\log\pi_{\theta }(y|x)\)
With some algebraic manipulation, we can rewrite the policy gradient in comparative form involving two responses to the same prompt. we name it Interactive policy gradient:
\(\mathbb{E}_{y_1,y_2\sim\pi_{\theta}}\left(r(y_1\vert x)-r(y_2\vert x)\right)\nabla\left(\log\ frac{\pi_\theta(y_1\vert x)}{\pi_\theta(y_2\vert x)}\right)/2\)
Unlike VPG, which relies directly on the absolute size of the reward, PPG uses reward differential. This allows you to bypass the compensated translation issue mentioned earlier. To further improve performance, we incorporate a playback buffer using: Importance Sampling Prevent large gradient updates by: clipping.
Importance sampling: Sample a set of responses from a playback buffer consisting of responses generated from \(\pi_{\text{old}}\) and then calculate the importance sampling rate for each response pair. The slope is the weighted sum of the slopes calculated from each pair of responses.
Clipping: Clips importance sampling rate and gradient updates to penalize overly large updates. This technique allows the algorithm to trade off the KL divergence and compensate more efficiently.
There are two ways to implement clipping techniques, divided into individual clipping or joint clipping. The resulting algorithm is called P3O (Pairwise Proximal Policy Optimization) and its variants are V1 or V2, respectively. More details can be found in the original document.
evaluation
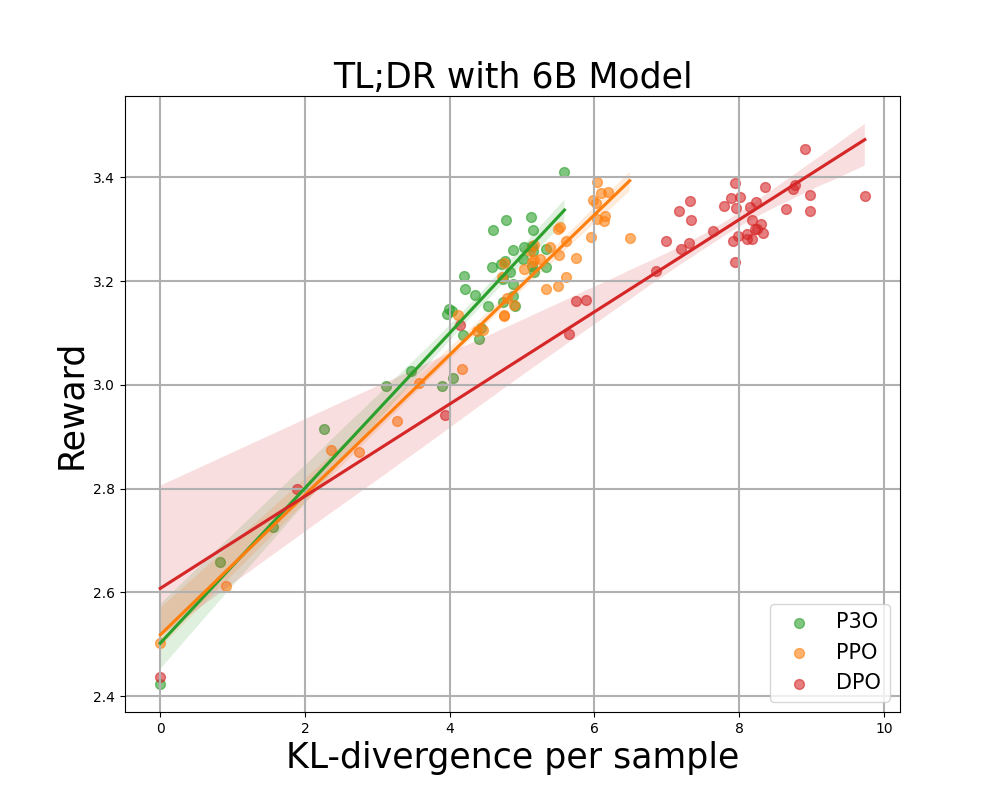
Figure 3:
KL-compensation frontier for TL;DR, by sequence Both KL and reward are averaged over 200 test prompts and calculated every 500 gradient steps. We found that a simple linear function fits the curve well. P3O has the best KL-Reward tradeoff among the three.
We explore two open text generation tasks. summary and Q & A. The summary leverages the TL;DR dataset where the \(x\) prompt is a forum post on Reddit and \(y\) is the corresponding summary. For question answering, we use Anthropic Helpful and Harmless (HH), where the prompts \(x\) are human queries on various topics, and the policy must learn how to generate attractive and useful responses \(y\).
Compare our algorithms P3O We use several effective and representative approaches for LLM alignment. we are SFT A policy learned with maximum likelihood. For RL algorithms, we consider the dominant approaches. PPO And the new proposed DPO. DPO directly optimizes the policy towards a closed solution of the KL-limited RL problem. Although proposed as an offline sorting method, we make it online using a surrogate compensation function.
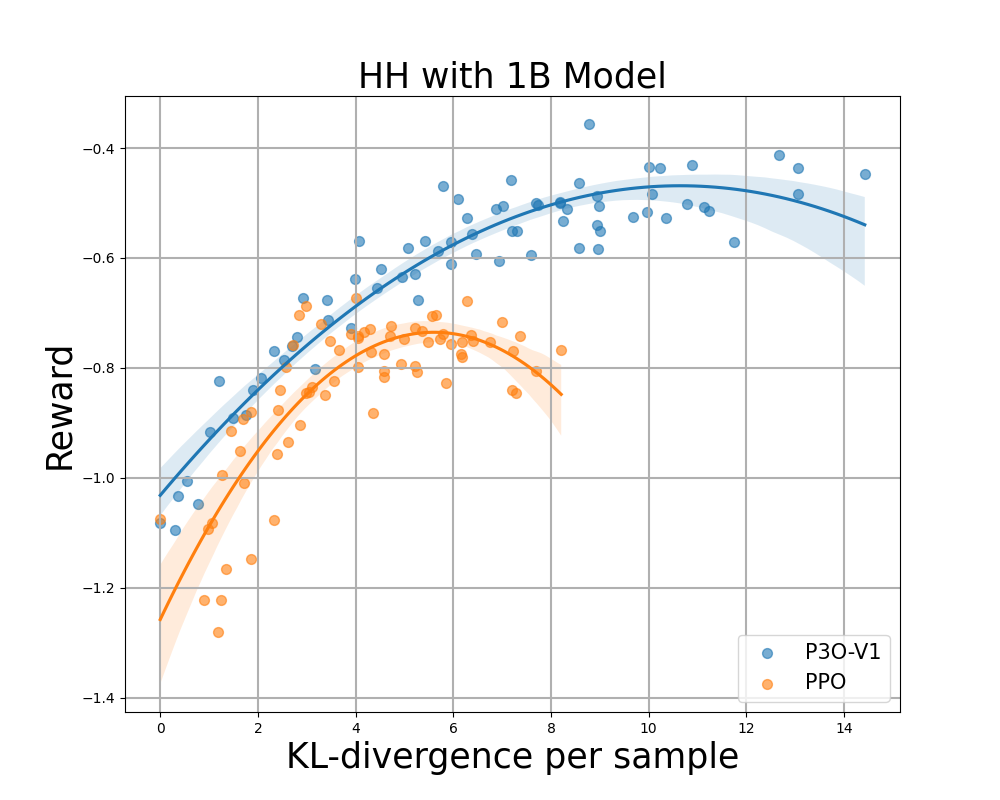
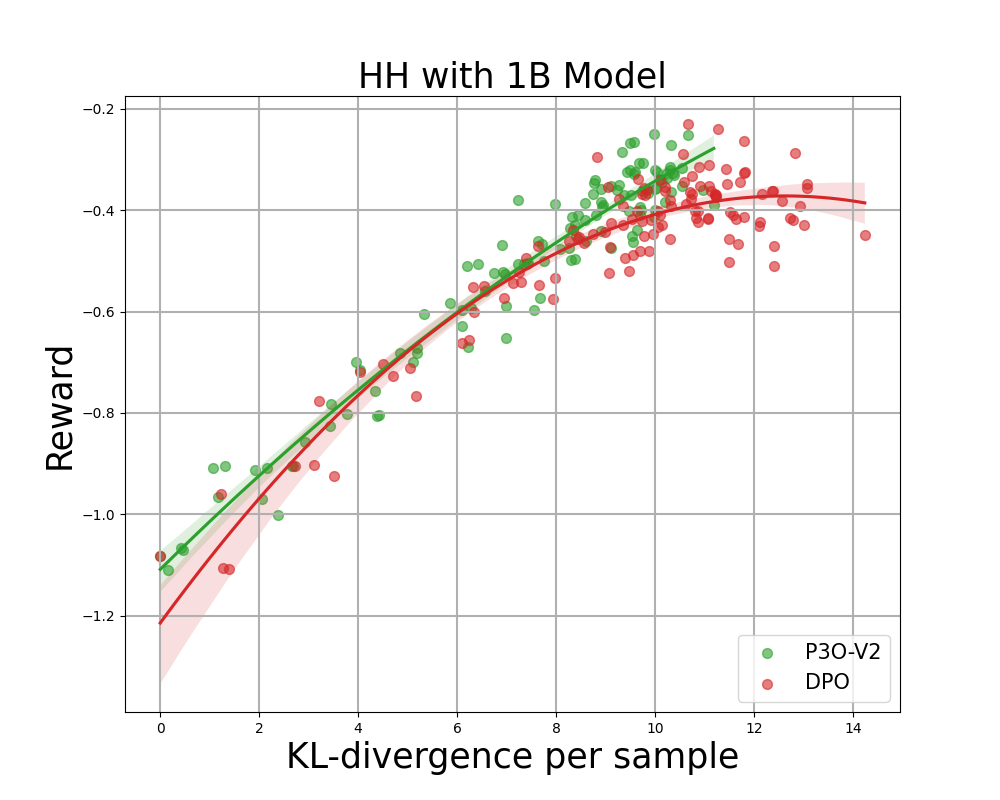
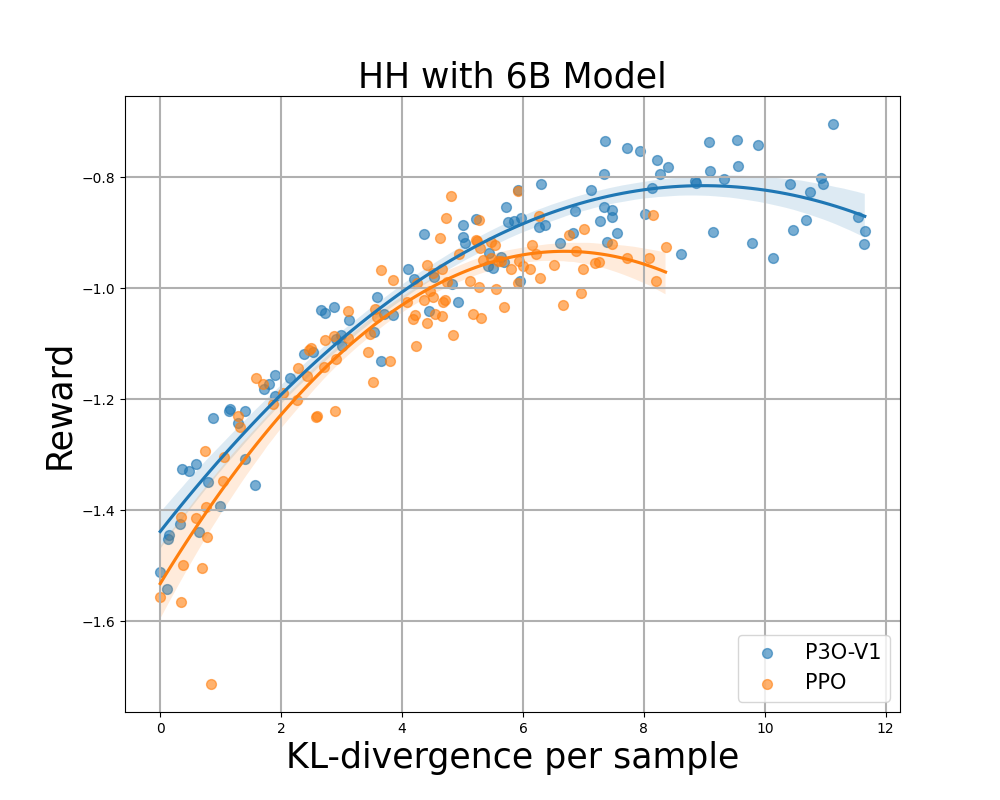
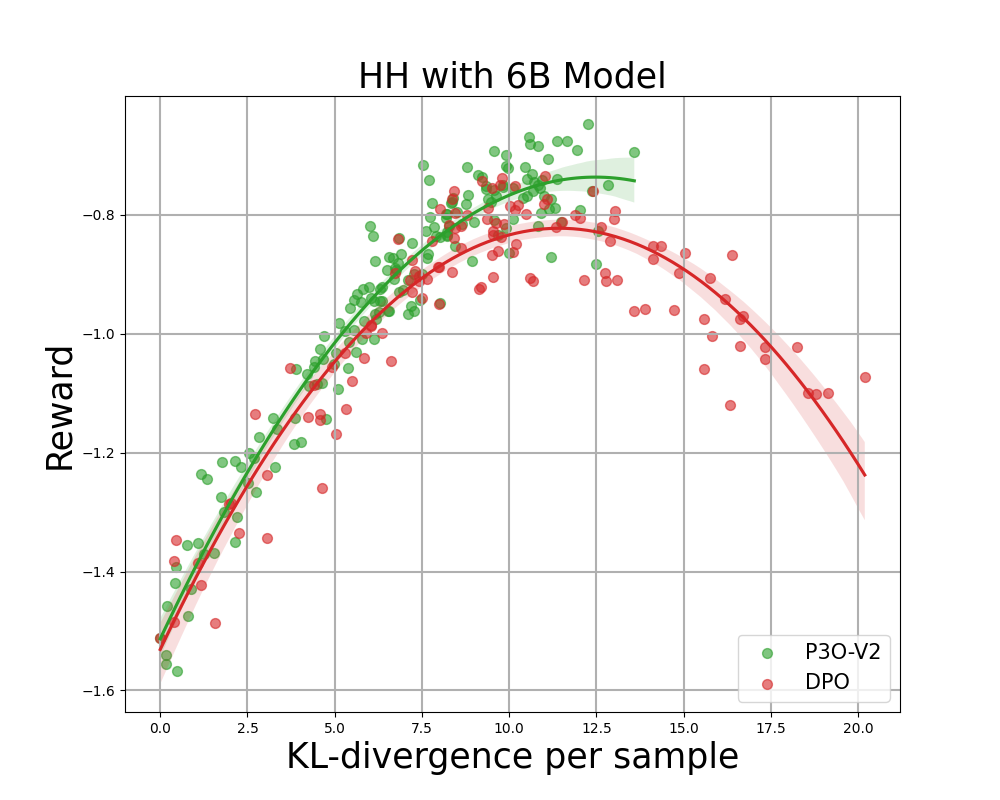
Figure 4:
KL-compensation frontier for HH, where each point represents the average result over 280 test prompts and is calculated every 500 gradient updates. The two figures on the left compare P3O-V1 and PPO at various base model sizes. The two pictures on the right compare P3O-V2 and DPO. The results show that P3O can not only obtain higher rewards but also provide better KL control.
Deviating too much from the reference policy will cause the online policy to cut corners in the reward model and produce inconsistent continuity, as pointed out in previous studies. We are interested not only in a well-established metric in the RL literature (compensation), but also in how far the learned policy deviates from the initial policy, as measured by KL-divergence. We therefore investigate the efficiency of each algorithm through the bounds of the achieved reward and its KL-divergence from the reference policy (KL-Rewards Frontier). From Figures 4 and 5, we find that P3O has strictly dominant bounds over PPO and DPO across a variety of model sizes.
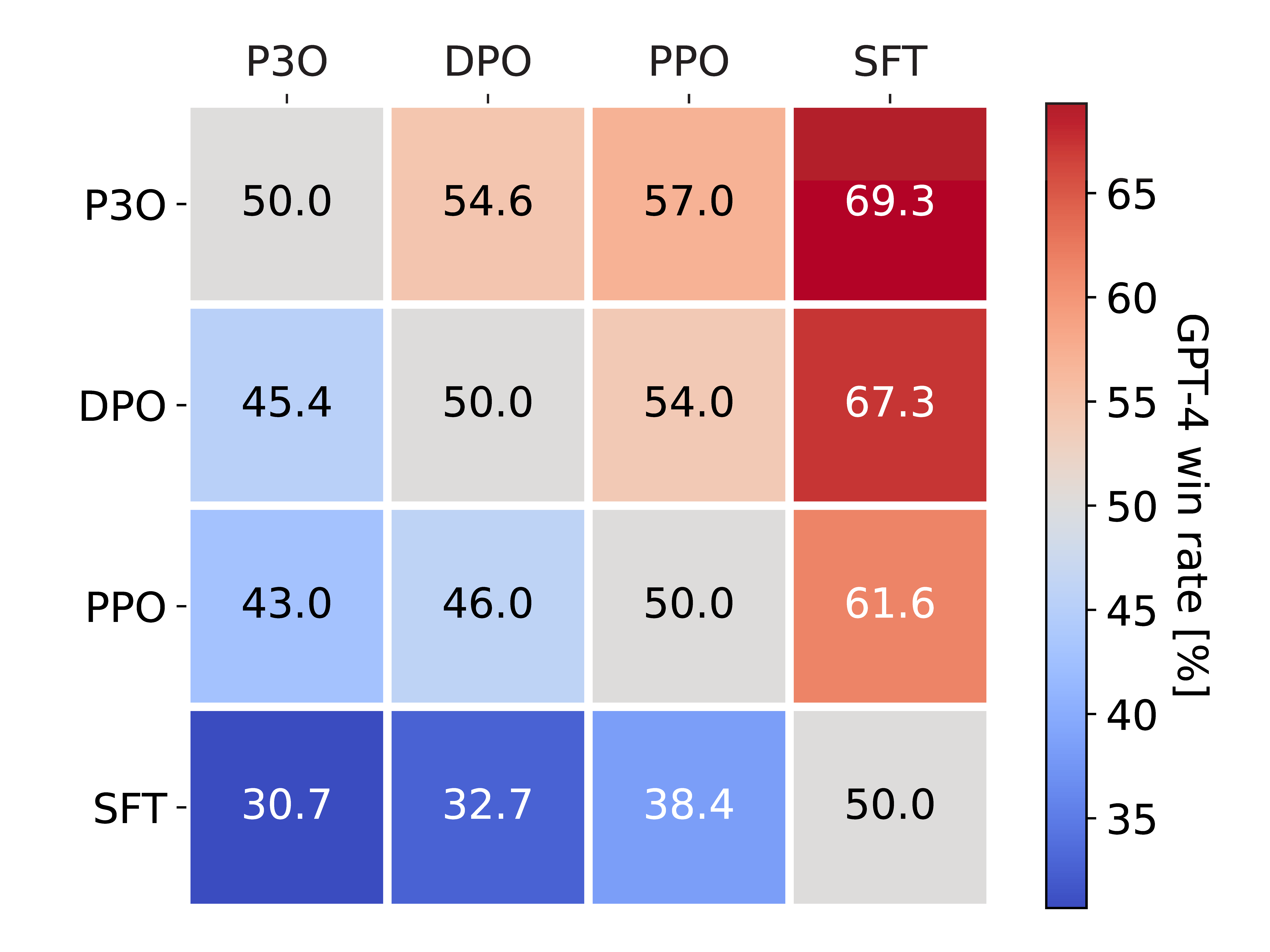
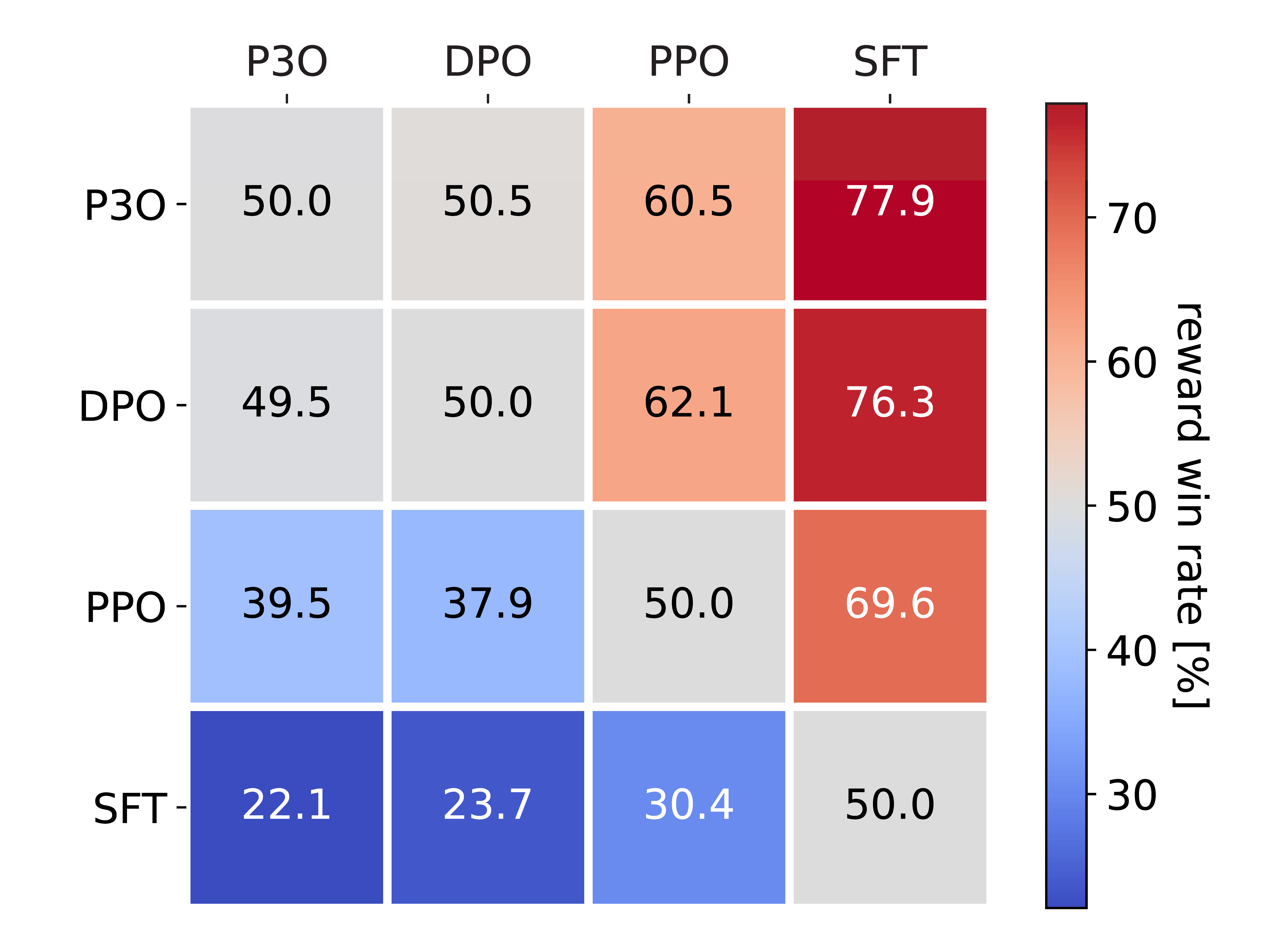
Figure 5:
The picture on the left displays the win rate evaluated by GPT-4. The picture on the right shows the win rates obtained by directly comparing proxy rewards. Despite the high correlation between the two numbers, we found that the reward odds had to be adjusted according to KL to match the GPT-4 odds.
To directly assess the quality of the generated response: One-to-one comparison Between all pairs of algorithms in the HH dataset. We use two indicators for evaluation: (1) compensationOptimized target during online RL, (2) GPT-4, as a faithful proxy for human evaluation of response usefulness. For the latter metric, we note that previous studies have shown that GPT-4 judgments are strongly correlated with humans, and that human agreement on GPT-4 is generally similar to or higher than inter-annotator agreement between humans.
Figure 5 shows comprehensive pairwise comparison results. The average KL divergence and reward ranking for this model is DPO > P3O > PPO > SFT. DPO slightly outperforms P3O in terms of reward, but has significantly higher KL-divergence, which can be detrimental to generation quality. As a result, DPO recorded a compensation win rate of 49.5% compared to P3O, but only 45.4% in GPT-4 evaluation. Compared to other methods, P3O has a GPT-4 win rate of 57.0% against PPO and 69.3% against SFT. These results are consistent with those of the KL-Reward frontier metric and confirm that P3O can better match human preferences than previous criteria.
conclusion
This blog post presents new insights into how to adapt large-scale language models to human preferences using reinforcement learning. We proposed a reinforcement learning framework with relative feedback, as shown in Figure 1. In this framework, we develop a new policy gradient algorithm, P3O. This approach integrates the basic principles of reward modeling and RL fine-tuning through comparative training. Our results show that P3O outperforms previous methods in terms of KL-Reward frontier and GPT-4 win rate.
Vivtex
This blog is based on recent papers and blogs. If this blog has inspired your work, consider citing it:
@article{wu2023pairwise,
title={Pairwise Proximal Policy Optimization: Harnessing Relative Feedback for LLM Alignment},
author={Wu, Tianhao and Zhu, Banghua and Zhang, Ruoyu and Wen, Zhaojin and Ramchandran, Kannan and Jiao, Jiantao},
journal={arXiv preprint arXiv:2310.00212},
year={2023}
}
