TLDR: we are Asymmetric authentication robustness This problem requires certified robustness for only one class and reflects a real-world adversarial scenario. This focused setup allows us to introduce a functional convex classifier that generates closed-form and deterministic authentication radii on the millisecond scale.

Figure 1. Illustration of feature convex classifier and authentication on sensitive class input. This architecture uses the learned convex function $g$ to construct a Lipschitz continuous feature map $\varphi$. Since $g$ is convex, it is globally underapproximated by the tangent plane of $\varphi(x)$, yielding a standard ball certified in the feature space. The Lipschitzness of $\varphi$ produces appropriately sized certificates in the original input space.
Despite their widespread use, deep learning classifiers are very vulnerable to: hostile example: Small, imperceptible image perturbations to humans that trick machine learning models into misclassifying modified inputs. These weaknesses seriously undermine the reliability of safety-critical processes that incorporate machine learning. Many heuristic defenses against enemy disruption have been proposed, but are often defeated by later, more powerful attack strategies. Therefore, we focus on: A truly powerful classifierThis provides a mathematical guarantee that the prediction for the $\ell_p$-norm ball around the input will remain constant.
Existing certified robustness methods lead to various drawbacks, including non-determinism, slow execution, poor scalability, and certification against only one attack standard. We argue that these problems can be addressed by improving the certified robustness problem to better suit realistic adversarial settings.
Asymmetric authentication robustness issues
Currently certifiable, strong classifiers generate certificates for inputs belonging to all classes. For many real-world adversarial applications, this is unnecessarily broad. Consider the example of someone writing a phishing scam email while trying to avoid spam filters. These attackers will always try to trick spam filters into thinking their spam emails are harmless. It’s never the other way around. In other words, The attacker is only trying to induce false negatives from the classifier.. Similar settings include detecting malware, flagging fake news, detecting social media bots, filtering health insurance claims, detecting financial fraud, detecting phishing websites, and more.
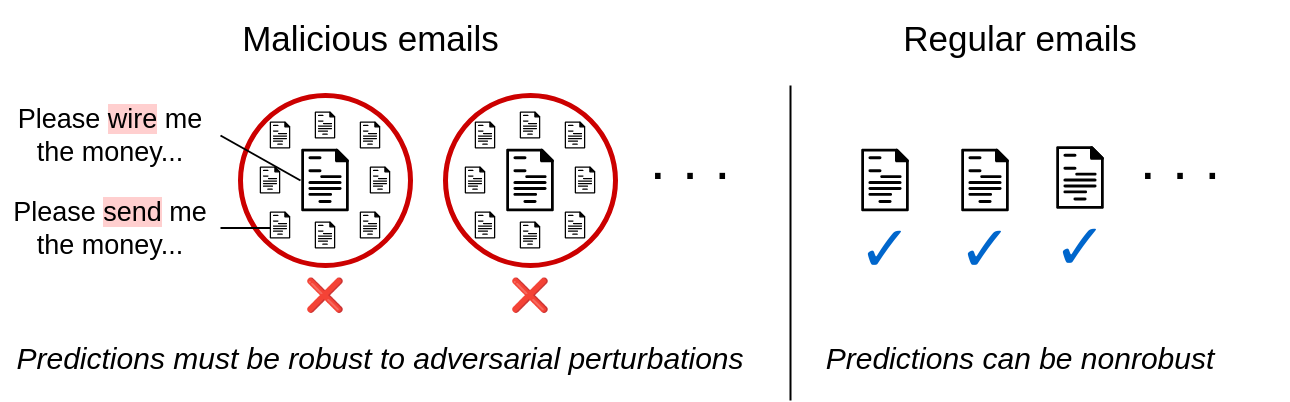
Figure 2. Asymmetric robustness of email filtering. Practical adversarial settings often require certified robustness for only one class.
These applications all include one binary classification setup. sensitive class What attackers are trying to avoid (e.g. the “spam email” class) This motivates the problem. Asymmetric authentication robustnessIt aims to provide authenticated and robust predictions for inputs of sensitive classes while maintaining high accuracy for all other inputs. We provide a more formal problem statement in the text.
Feature – Convex Classifier
we suggest Features convex neural network Addresses the asymmetric robustness problem. This architecture uses a trained Input-Convex Neural Network (ICNN) ${g: \mathbb to create a simple Lipschitz continuous feature map ${\varphi: \mathbb{R}^d \to \mathbb{R}^q}$ Configure . {R}^q \to \mathbb{R}}$ (Figure 1). ICNN constructs the ReLU nonlinearity with a non-negative weight matrix to enforce convexity from input to output logit. Since the binary ICNN decision domain consists of a convex set and its complement, we add a pre-constructed feature map $\varphi$ to allow for non-convex decision domains.
Using a feature-convex classifier, we can quickly compute sensitive class authentication radii for all $\ell_p$-norms. Using the fact that the convex function is globally underapproximated by the tangent plane, we can obtain the authenticated radius in the intermediate feature space. This radius is propagated into the input space by Lipschitzness. Asymmetrical settings are very important here. This is because this architecture only generates certificates for positive logit classes $g(\varphi(x)) > 0$.
The resulting $\ell_p$-norm authentication radius formula is particularly elegant.
\(r_p(x) = \frac{ \color{blue}{g(\varphi(x))} } { \mathrm{Lip}_p(\varphi) \color{red}{\| \nabla g(\ varphi(x)) \| _{p,*}}}.\)
Non-constant terms are easy to interpret. The radius is Classifier confidence and vice versa Classifier sensitivity. We evaluate these certificates across a variety of datasets to obtain $\ell_2$ and $\ell_{\infty}$ certificates that are similar to the competitive $\ell_1$ certificate. Despite other methods that are usually tailored to specific standards and require much more runtime.
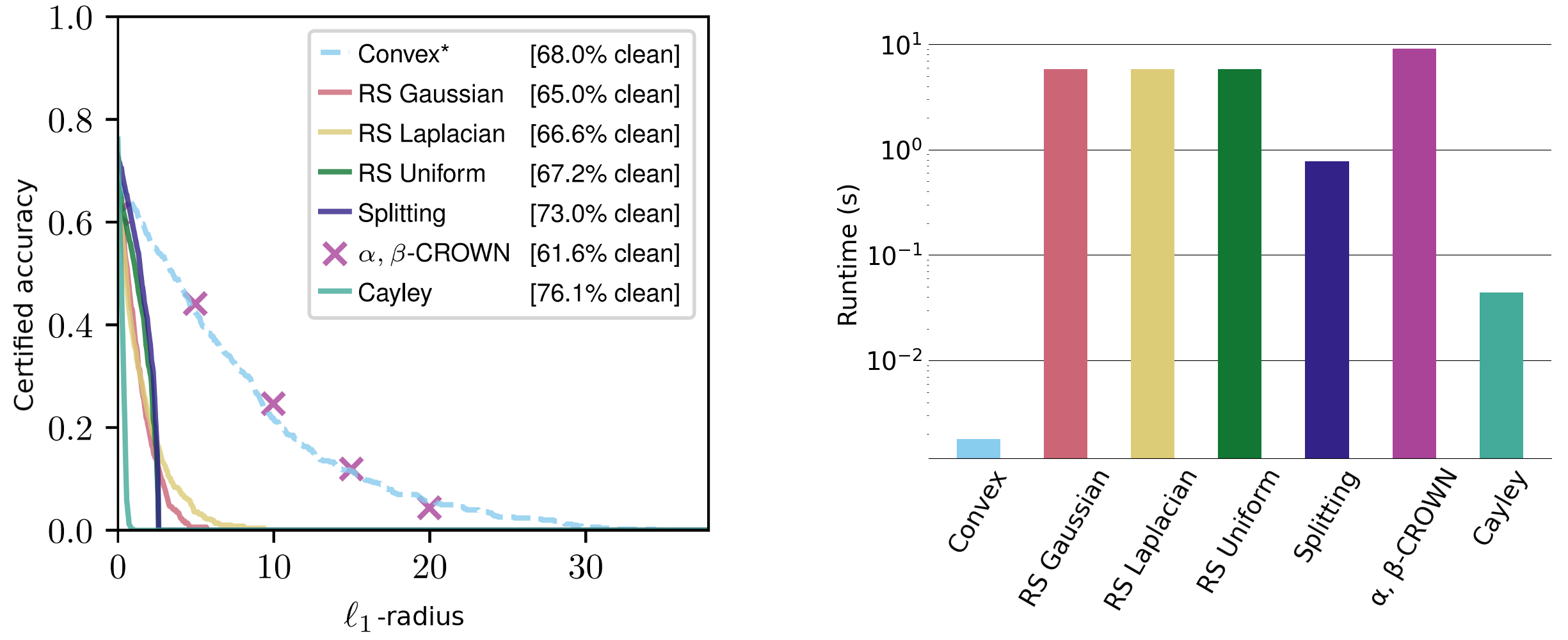
Figure 3. Sensitive class authentication radius of the CIFAR-10 cat vs. dog dataset for $\ell_1$-norm. Runtimes on the right are averaged over $\ell_1$, $\ell_2$, and $\ell_{\infty}$-radii (see log scaling).
Our certificate applies to all $\ell_p$-norm and is closed and deterministic, requiring only one forward and backward pass per input. This can be calculated in milliseconds and scales with network size. For comparison, current state-of-the-art methods such as random smoothing and gap boundary propagation typically take several seconds to authenticate small networks. Random smoothing methods are also inherently non-deterministic, using certificates that are maintained with high probability.
theoretical promise
Although initial results are promising, our theoretical work suggests that even without feature maps, there is significant untapped potential in ICNNs. We demonstrate that, despite the binary ICNN being limited to convex decision region learning, there is an ICNN that achieves perfect training accuracy on the CIFAR-10 cats-vs-dogs dataset.
actually. We have an input convex classifier that achieves perfect training accuracy on the CIFAR-10 cat vs. dog dataset.
However, our architecture achieves $73.4\%$ training accuracy without feature maps. Although training performance does not imply test set generalization, these results suggest that ICNN can, at least theoretically, achieve state-of-the-art machine learning paradigms that overfit the training dataset. We therefore raise the following open questions in this area:
The question is open. Discover an input convex classifier that achieves perfect training accuracy on the CIFAR-10 cat vs. dog dataset.
conclusion
We hope that our asymmetric robustness framework will inspire new architectures that are certifiable in more focused environments. Our feature-convex classifier is one such architecture and provides fast and deterministic certified radii for any $\ell_p$-norm. We also raise the open problem of overfitting the CIFAR-10 cats versus dogs training dataset using ICNN, showing that it is theoretically possible.
This post is based on the following paper:
Asymmetric authentication robustness via functional convex neural networks.
Samuel PommerBrandon G. AndersonJulien Piet, Somaye Sojudi,
37th Neural Information Processing Systems Conference (NeurIPS 2023).
More information is available on arXiv and GitHub. If our paper has inspired your work, please cite it as follows:
@inproceedings{
pfrommer2023asymmetric,
title={Asymmetric Certified Robustness via Feature-Convex Neural Networks},
author={Samuel Pfrommer and Brendon G. Anderson and Julien Piet and Somayeh Sojoudi},
booktitle={Thirty-seventh Conference on Neural Information Processing Systems},
year={2023}
}
